Manipulation du signe somme

III Sommation d'un ensemble fini de valeurs

I Généralités

x_{1}, x_{2}, . . ., x_{7}

désignent

7

nombres, leur somme s'écrit

S = x_{1} + x_{2} + . . . + x_{7}

ou de façon plus synthétique :

$S = \sum_{i = 1}^{7} x_{i} .$

On lit l'expression

S = \sum_{i = 1}^{7} x_{i}

: S est égal à la somme des

x_{i}

pour

i

parcourant tous les entiers de 1 à 7.
La somme des nombres

x_{5}

x_{6}

,...,

x_{6}

x_{7}

s'écrit

x_{5} + . . . + x_{7}

ou de façon plus synthétique :

S = \sum_{i = 5}^{7} x_{i}

.
Exemple

Une compétition comporte

6

épreuves. Le tableau suivant décrit le score

x_{i}

qu'un enfant a eu à la

i

-ième épreuve :

$x_{1}$	$x_{2}$	$x_{3}$	$x_{4}$	$x_{5}$	$x_{6}$
5	10	4	3	9	10

Le total des points obtenus lors de cette compétition s'écrit :

\sum_{i = 1}^{6} x_{i} = 5 + 10 + 4 + 3 + 9 + 10 = 41

.
Le total des points obtenus sur les 4 dernières épreuves s'écrit :

\sum_{i = 3}^{6} x_{i} = 4 + 3 + 9 + 10 = 16

De manière générale, si

a

b

sont deux entiers avec

a \leq b

\sum_{i = a}^{b} x_{i}

est la somme des

x_{i}

pour

i

parcourant tous les entiers de

a

b

. On écrit aussi

$\sum_{i = a}^{b} x_{i} = \sum_{a \leq i \leq b} x_{i} .$

Exemple

Pour tout réel

u

$\sum_{i = 1}^{7} u = 7 u .$

Exemple

$\sum_{i = 1}^{7} i = 1 + 2 + \dots + 7 = 28 .$

N.B

L'indice $i$ dans les sommes précédentes est ce qu'on appelle un indice muet :
$S = \sum_{j = 1}^{7} x_{j} = \sum_{k = 1}^{7} x_{k} = \sum_{r = 1}^{7} x_{r} .$

Voici d'autres expressions équivalentes de $S$ :
$S = \sum_{h = 0}^{6} x_{1 + h} = \sum_{k = 1}^{7} x_{8 - k} .$
Dans la notation $\sum_{i = a}^{b} x_{i}$ , $a$ désigne la plus petite valeur que prend l'indice $i$ et $b$ désigne la plus grande valeur que prend l'indice $i$ ; l'indice $i$ va parcourir les entiers de $a$ à $b$ .
Si on rencontre une somme $\sum_{i = a}^{b} x_{i}$ avec $a > b$ , on donne à la somme la valeur 0.

Propriétés

Soient

x_{1}, x_{2}, . . ., x_{n}

y_{1}, y_{2}, . . ., y_{n}

c

des nombres réels. Alors

\begin{matrix} \sum_{i = 1}^{n} c x_{i} = c \sum_{i = 1}^{n} x_{i} & (traduction de c x_{1} + c x_{2} = c (x_{1} + c x_{2}) si n = 2) \\ \sum_{i = 1}^{n} (x_{i} + y_{i}) = \sum_{i = 1}^{n} x_{i} + \sum_{i = 1}^{n} y_{i} & (traduction de (x_{1} + y_{1}) + (x_{2} + y_{2}) = (x_{1} + x_{2}) + (y_{1} + y_{2}) si n = 2) \end{matrix}

II Sommes classiques

Proposition [Somme arithmétique]

Pour tout entier positif

n

, on a

$\sum_{i = 1}^{n} i = \frac{n (n + 1)}{2} .$

Preuve

Ecrivons la somme deux fois en écrivant les termes une fois dans l'ordre croissant et une fois dans l'ordre décroissant :

$2 \sum_{i = 1}^{n} i$	=	1	+	2	+		+	(n-1)	+	n
	+	n	+	(n - 1)	+		+	2	+	1

En sommant deux par deux les termes qui apparaissent l'un en dessous de l'autre, on obtient à chaque fois

n + 1

. Donc,

2 \sum_{i = 1}^{n} i = n (n + 1) .

Proposition [Somme géométrique]

Soit

a

un réel différent de 1. Pour tout un entier positif

n

, on a

$\sum_{i = 0}^{n} a^{i} = \frac{1 - a^{n + 1}}{1 - a} = \frac{a^{n + 1} - 1}{a - 1} .$

Preuve

Développons le produit

T = (1 - a) (\sum_{i = 0}^{n} a^{i})

\begin{matrix} T & = & (1 - a) (1 + a + a^{2} + \dots + a^{n}) \\ = & (1 - a) + (a - a^{2}) + (a^{2} - a^{3}) + \dots + (a^{n} - a^{n + 1}) . \end{matrix}

Lorsqu'on simplifie, il reste le premier terme et le dernier terme dans le développement de

T

, ce qui donne

T = 1 - a^{n + 1}

.
On peut aussi faire la démonstration en utilisant la notation compacte :

\begin{aligned} T & = (1 - a) (\sum_{i = 0}^{n} a^{i}) = \sum_{i = 0}^{n} a^{i} - a \sum_{i = 0}^{n} a^{i} \\ = \sum_{i = 0}^{n} a^{i} - \sum_{i = 0}^{n} a^{i + 1} = \sum_{i = 0}^{n} a^{i} - \sum_{i = 1}^{n + 1} a^{i + 1} \\ = a^{0} - a^{n + 1} = 1 - a^{n + 1} \end{aligned}

Exercice

Soit

k

n

des entiers positifs tels que

k < n

et soit

a

un réel différent de 1. Trouver l'expression de

$U = \sum_{i = k}^{n} a^{i} .$

Indications

On peut se ramener à l'expression donnée dans la proposition , en faisant le changement de variable

j = i - k

Solution

On se ramène à l'expression donnée dans la proposition , en faisant le changement de variable $j = i - k$ .
$U = \sum_{j = 0}^{n - k} a^{k + j} .$
Comme $a^{k + j} = a^{k} a^{j}$ pour tout entier $j$ , on a :
$U = a^{k} \sum_{j = 0}^{n - k} a^{j} .$
Il reste à utiliser la proposition :
$U = a^{k} \frac{1 - a^{n + 1 - k}}{1 - a} = \frac{a^{k} - a^{n + 1}}{1 - a} = \frac{a^{n + 1} - a^{k}}{a - 1} .$

Exercice [Somme des n premiers carrés d'entiers]

Soit

n

un entier strictement positif. Montrer que

\sum_{i = 1}^{n} i^{2} = \frac{1}{6} n (n + 1) (2 n + 1) .

Indications

On pourra d'abord simplifier

\sum_{i = 1}^{n} ((i + 1)^{3} - i^{3})

, puis réécrire cette somme différemment, en développant le terme

(i + 1)^{3}

afin de faire apparaître la somme

\sum_{i = 1}^{n} i^{2}

. On en déduit alors l'expression de

\sum_{i = 1}^{n} i^{2}

Solution

Déjà

\sum_{i = 1}^{n} ((i + 1)^{3} - i^{3}) = (n + 1)^{3} - 1

. D'autre part

(i + 1)^{3} = i^{3} + 3 i^{2} + 3 i + 1

. Donc,

$\sum_{i = 1}^{n} ((i + 1)^{3} - i^{3}) = 3 \sum_{i = 1}^{n} i^{2} + 3 \sum_{i = 1}^{n} i + n .$

D'après la proposition ,

\sum_{i = 1}^{n} i = \frac{1}{2} n (n + 1) .

On en déduit que

$\sum_{i = 1}^{n} i^{2} = \frac{1}{3} ((n + 1)^{3} - 1 - \frac{3}{2} n (n + 1) - n) .$

En mettant

\frac{1}{6} (n + 1)

en facteur dans le terme de droite, on obtient

$\sum_{i = 1}^{n} i^{2} = \frac{1}{6} (n + 1) (2 (n + 1)^{2} - 3 n - 2)$

On trouve l'expression annoncée en remarquant que

2 (n + 1)^{2} - 3 n - 2 = 2 n^{2} + n = n (2 n + 1)

III Sommation d'un ensemble fini de valeurs

Lorsqu'on somme un nombre fini de valeurs, on peut changer l'ordre dans lequel on somme les différents nombres sans que cela change le résultat puisque, si

a

b

sont deux nombres réels alors

a + b

b + a

. On peut donc aussi utiliser une notation abrégée qui ne précise pas l'ordre dans lequel on somme les valeurs : si

X

désigne l'ensemble formé des

14

nombres

x_{1}, \dots, x_{14}

, la somme

$S = \sum_{i = 1}^{14} x_{i}$

peut aussi s'écrire :

$S = \sum_{u \in X} u .$

Exemple

$\sum_{i \in {1, 3, 5, 9}} x_{i} = x_{1} + x_{3} + x_{5} + x_{9}$

$\sum_{i \in {1, 2, 3}} x_{i} = \sum_{1 \leq i \leq 3} x_{i} = \sum_{i = 1}^{3} x_{i}$

Propriétés

Soit

A

un ensemble fini de réels.

Pour tout réel $c$ ,
$\sum_{x \in A} cx = c \sum_{x \in A} x .$
Si $f$ et $g$ sont deux fonctions définies sur $A$ alors
$\sum_{x \in A} (f (x) + g (x)) = \sum_{x \in A} f (x) + \sum_{x \in A} g (x) .$
Si $B$ est un sous-ensemble de $A$ dont le complémentaire dans $A$ est noté $A ∖ B$ , alors
$\sum_{x \in A} x = \sum_{y \in B} y + \sum_{z \in A ∖ B} z .$
Plus généralement, pour n'importe quelle fonction $f$ définie sur $A$ ,
$\sum_{x \in A} f (x) = \sum_{y \in B} f (y) + \sum_{z \in A ∖ B} f (z) .$

Exemple

On note

A

l'ensemble des entiers (négatifs ou positifs) dont la valeur absolue est inférieure ou égale à

20

. Déterminer :

la somme des éléments de $A$ , c'est-à-dire : $I = \sum_{a \in A} a$ .
la somme des carrés des éléments de $A$ , c'est-à-dire : $J = \sum_{a \in A} a^{2} .$

Solution

IV Sommes doubles

Soit

X

un ensemble fini et

f

une fonction définie sur

X

et à valeurs dans

ℝ

. Pratiquement, si on veut calculer

S = \sum_{x \in X} f (x)

qui correspond à la somme des valeurs de

f (x)

lorsque

x

parcourt l'ensemble

X

, il faut choisir l'ordre dans lequel on parcourt les éléments de

X

.
Dans le cas où

X

est un sous-ensemble de

ℝ

, il existe un ordre naturel : on peut par exemple parcourir les éléments de

X

par ordre croissant.

Exemple

X = {- 1, 1, 3, 5}

alors

\sum_{x \in X} f (x) = f (- 1) + f (1) + f (3) + f (5)

. Si

X

est l'ensemble des entiers compris entre

- 14

14

alors

\sum_{x \in X} f (x) = \sum_{i = - 14}^{14} f (i)

Dans le cas où

X

est un sous-ensemble de

ℝ^{2}

, les éléments de

X

peuvent être représentés comme des points sur le plan. Nous allons détailler deux façons classiques de parcourir les éléments de

X

, mais il en existe d'autres.

On peut décomposer $X$ en sous-ensembles d'éléments qui ont même abscisse et parcourir les éléments de ces sous-ensembles par ordre croissant de leur ordonnée. On décompose ainsi le calcul en faisant successivement deux sommes.

Exemple
Si $X = {1, 2, \dots, 14} \times {1, 2, \dots, 7}$ alors
$\sum_{(i, j) \in X} f (i, j) = \sum_{i = 1}^{14} (\sum_{j = 1}^{7} f (i, j)) .$
C'est une façon compacte d'écrire :
$\begin{matrix} \sum_{(i, j) \in X} f (i, j) & = & f (1, 1) & + & f (1, 2) & + \dots + & f (1, 7) \\ + & f (2, 1) & + & f (2, 2) & + \dots + & f (2, 7) \\ ⋮ & ⋮ & ⋮ \\ + & f (14, 1) & + & f (14, 2) & + \dots + & f (14, 7) \end{matrix}$
On peut aussi décomposer $X$ en sous-ensembles d'éléments qui ont même ordonnée et parcourir les éléments de ces sous-ensembles par ordre croissant de leur abscisse.
Exemple
Si $X = {1, 2, \dots, 14} \times {1, 2, \dots, 7}$ alors
$\sum_{(i, j) \in X} f (i, j) = \sum_{j = 1}^{7} (\sum_{i = 1}^{14} f (i, j)) .$
C'est une façon compacte d'écrire :
$\begin{matrix} \sum_{(i, j) \in X} f (i, j) & = & f (1, 1) & + & f (2, 1) & + \dots + & f (14, 1) \\ + & f (1, 2) & + & f (2, 2) & + \dots + & f (14, 2) \\ ⋮ & ⋮ & ⋮ \\ + & f (1, 7) & + & f (2, 7) & + \dots + & f (14, 7) \end{matrix}$

Exemple

Considérons l'ensemble

X = {(i, j) \in {1, 2, \dots, 6} \times {1, 2, \dots, 6}, tel que j \leq i}

. La première méthode de décomposition de

X

proposée consiste à parcourir les points dans l'ordre suggéré par le dessin.

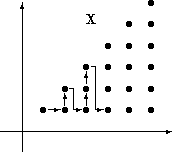Cela revient à écrire

$\sum_{(i, j) \in X} f (i, j) = \sum_{i = 1}^{6} (\sum_{j = 1}^{i} f (i, j)) .$

La deuxième méthode de décomposition de

X

proposée consiste à parcourir les points dans l'ordre suggéré par le dessin suivant.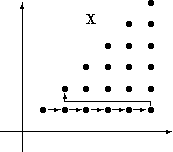

Cela revient à écrire

$\sum_{(i, j) \in X} f (i, j) = \sum_{j = 1}^{6} (\sum_{i = j}^{6} f (i, j)) .$

document.
: , serveur interactif, enseignement, cours en ligne, ressources pédagogiques, sciences, langues, qcm,classes,exercices

Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.